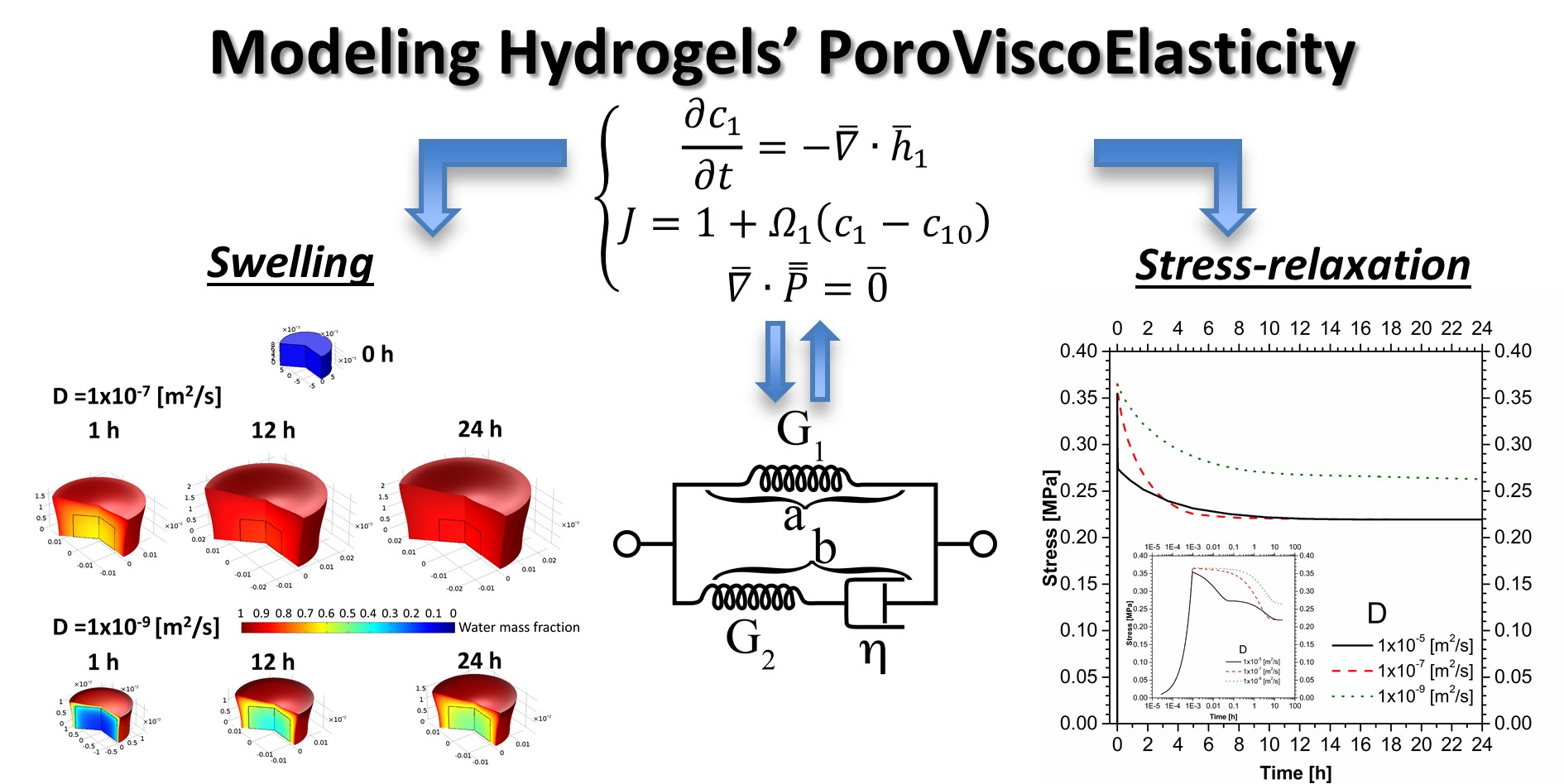
In the following a 15 minutes video guide to show a very basic implementation in COMSOL Multiphysics of the poroviscoelastic model proposed in “Caccavo D. & Lamberti G. (2017). PoroViscoElastic model to describe hydrogels’ behavior. Materials Science and Engineering: C 76: 102-113, DOI: 10.1016/j.msec.2017.02.155 ”.
Aim of this guide is to provide an initial aid in the implementation of the model, therefore facilitating its use and spreading across the scientific community. We DO NOT provide specific aid for numerical issues and convergence problems.
The parameters, variables and equations files can be downloaded at the bottom of this page.
The file “Variables expressions using MATLAB” can be run in MATLAB to obtain the expressions of the variables used in the model development. It is not directly needed for the model implementation but it could be very useful when the constitutive equations have to be modified.